Kalkulator dwumianu Newtona
Kalkulator dwumianu Newtona
Dwumian Newtona dla wprowadzonych n i k:
Dwumian Newtona (znany również jako współczynnik dwumianowy lub liczba kombinacji) to ważne pojęcie matematyczne, które określa liczbę sposobów wyboru k elementów ze zbioru n elementów bez powtórzeń i bez względu na kolejność.
Nasz kalkulator umożliwia błyskawiczne obliczenie wartości dwumianu Newtona dla dowolnych wartości n i k. Wystarczy wprowadzić odpowiednie liczby, a wynik pojawi się automatycznie.
Czym jest dwumian Newtona?
Definicja
Dwumian Newtona to liczba różnych sposobów wyboru k elementów z n-elementowego zbioru, bez uwzględniania kolejności i bez powtórzeń.
Oznacza się go symbolem:
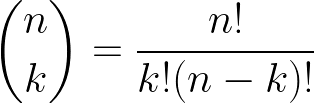
Inne nazwy
Dwumian Newtona znany jest również jako:
- Współczynnik dwumianowy
- Symbol Newtona
- Liczba kombinacyjna
- Liczba kombinacji n po k (n wybierz k)
- Współczynnik Newtona
- Współczynnik kombinatoryczny
Jak obliczyć dwumian Newtona?
Obliczanie dwumianu Newtona sprowadza się do zastosowania wzoru:
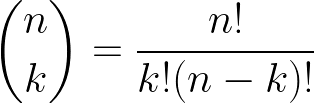
gdzie:
- n! to silnia liczby n (iloczyn wszystkich liczb całkowitych od 1 do n)
- k! to silnia liczby k
- (n-k)! to silnia różnicy n i k
Powyższy wzór jest jednak trudny do bezpośredniego zastosowania dla dużych wartości, dlatego w praktyce stosuje się zoptymalizowane algorytmy obliczeniowe.
Przykłady obliczeń dwumianu Newtona
| n | k | Dwumian Newtona | Przykład interpretacji |
|---|---|---|---|
| 5 | 2 | 10 | Liczba sposobów wyboru 2 osób z grupy 5 osób |
| 10 | 3 | 120 | Liczba sposobów wyboru 3 pytań z 10 w teście |
| 7 | 0 | 1 | Jest tylko jeden sposób na wybranie 0 elementów |
| 6 | 6 | 1 | Jest tylko jeden sposób na wybranie wszystkich elementów |
| 49 | 6 | 13 983 816 | Liczba możliwych wyników w loterii (6 z 49) |
Zastosowania dwumianu Newtona
Matematyka i statystyka
- Rozwijanie wyrażeń algebraicznych
- Twierdzenie dwumianowe
- Rozkłady prawdopodobieństwa
- Testy statystyczne
- Teoria gier i decyzji
Informatyka i algorytmika
- Kryptografia
- Teoria kodowania
- Kompresja danych
- Analiza algorytmów
- Kombinatoryka obliczeniowa
Zastosowania praktyczne
- Obliczanie prawdopodobieństwa w loteriach
- Analiza ryzyka
- Planowanie eksperymentów
- Genetyka i biologia molekularna
- Sterowanie i optymalizacja systemów
Podsumowanie
Dwumian Newtona to fundamentalne pojęcie w matematyce, które znajduje zastosowanie w wielu dziedzinach nauki i praktyki. Określa on liczbę sposobów wyboru podzbioru o określonej liczebności z danego zbioru.
Nasz kalkulator dwumianu Newtona umożliwia szybkie i bezproblemowe obliczanie wartości dla dowolnych poprawnych danych wejściowych. Bez względu na to, czy potrzebujesz tych obliczeń do matematyki, statystyki, informatyki czy planowania loterii - nasze narzędzie dostarczy Ci precyzyjnych wyników w ułamku sekundy.