Kalkulator logarytmów - szybkie obliczenia online
Kalkulator logarytmów
Jak to działa?
Logarytm o podstawie b z liczby a (zapisywany jako logba) to wykładnik potęgi, do której należy podnieść liczbę b, aby otrzymać liczbę a.
logba = c ⟺ bc = a
Kalkulator logarytmów to intuicyjne narzędzie online, które umożliwia błyskawiczne obliczenia logarytmów dowolnego typu. Bez względu na to, czy potrzebujesz logarytmu naturalnego (ln), dziesiętnego (log10) czy o specyficznej podstawie - nasz kalkulator dostarczy precyzyjnych wyników w ułamku sekundy.
Wystarczy wprowadzić liczbę i wybrać podstawę logarytmu, a wynik pojawi się natychmiast. Z dokładnością do 10 miejsc po przecinku, narzędzie to jest idealne zarówno dla uczniów i studentów, jak i dla profesjonalistów z dziedzin naukowych i technicznych.
Jak korzystać z kalkulatora logarytmów?
Proste kroki obliczania logarytmów
- Wprowadź liczbę, dla której chcesz obliczyć logarytm (musi być dodatnia)
- Wybierz podstawę logarytmu:
- Kliknij przycisk "10" dla logarytmu dziesiętnego
- Kliknij przycisk "e" dla logarytmu naturalnego
- Kliknij przycisk "2" dla logarytmu binarnego
- Lub wprowadź własną podstawę (musi być dodatnia i różna od 1)
- Ustaw preferowaną dokładność wyniku (liczba miejsc po przecinku)
- Otrzymaj natychmiastowy wynik logarytmu
Co możesz obliczyć?
- Logarytm naturalny (ln) - wykorzystywany w analizach wzrostu wykładniczego i fizyce
- Logarytm dziesiętny (log10) - powszechny w pomiarach akustycznych i sejsmicznych
- Logarytm binarny (log2) - kluczowy w informatyce i analizie algorytmów
- Logarytmy o dowolnej podstawie - dla specjalistycznych zastosowań
Zrozumieć logarytmy - kluczowe informacje
Definicja logarytmu
Dla liczb a i b gdzie a, b > 0 oraz a ≠ 1, logarytmem o podstawie a z liczby b nazywamy liczbę rzeczywistą x spełniającą równanie:
Zapisujemy to jako: logab = x
Logarytm jest więc pytaniem: "Do jakiej potęgi należy podnieść podstawę a, aby otrzymać liczbę b?" Jest działaniem odwrotnym do potęgowania.
Logarytm dziesiętny (log10)
Nazywany również logarytmem briggsowskim (od Henry'ego Briggsa, który wprowadził go w 1614 roku).
Przykład: log101000 = 3, ponieważ 103 = 1000
Logarytm naturalny (ln)
Logarytm o podstawie e (liczba Eulera ≈ 2,718281828459).
Przykład: ln(e²) = 2, ponieważ e2 = e²
Logarytm binarny (log2)
Szczególnie ważny w informatyce i teorii informacji.
Przykład: log28 = 3, ponieważ 23 = 8
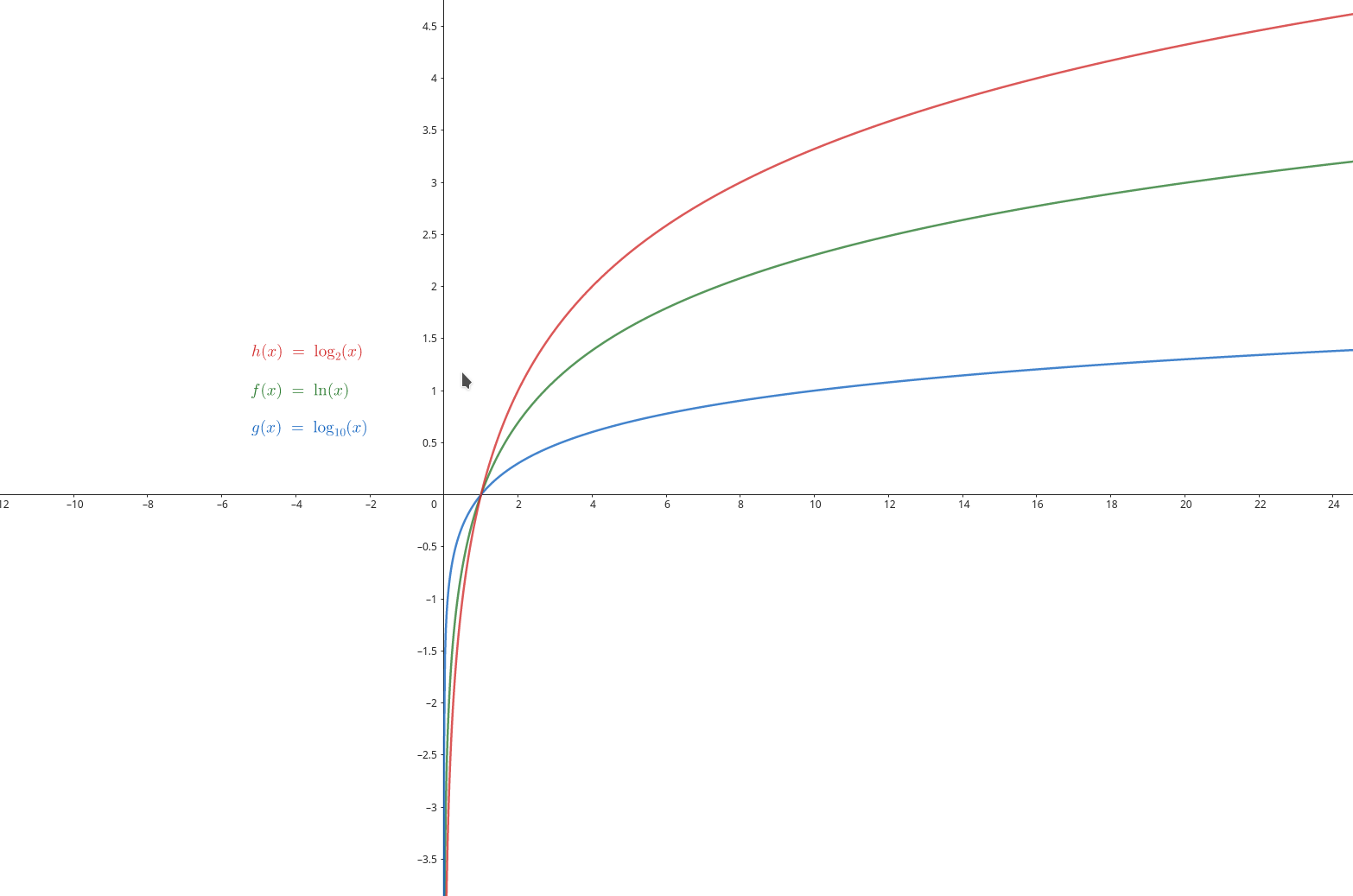
Na powyższym wykresie: ln(x) - logarytm naturalny, log2(x) - logarytm o podstawie 2, log10(x) - logarytm dziesiętny
Właściwości logarytmów
Podstawowe właściwości
- Logarytm z 1: loga1 = 0 (dla dowolnej podstawy a)
- Logarytm z podstawy: logaa = 1
- Logarytm z potęgi: loga(xn) = n × logax
Reguły operacyjne
- Logarytm iloczynu: loga(x×y) = logax + logay
- Logarytm ilorazu: loga(x/y) = logax - logay
- Zmiana podstawy: logax = logbx / logba
Skala logarytmiczna - wizualizacja danych
Skala logarytmiczna to sposób wizualizacji danych, który pozwala na efektywne przedstawienie wartości różniących się o wiele rzędów wielkości na jednym wykresie.
Kluczowe cechy skali logarytmicznej:
- Równe odcinki na skali reprezentują równe mnożniki wartości (a nie równe przyrosty)
- Odległość między 1 a 10 jest taka sama jak między 10 a 100 czy 100 a 1000
- Zmiany procentowe są reprezentowane jako równe odległości
Zastosowania skali logarytmicznej:
- Wizualizacja danych astronomicznych (odległości gwiazd, masy planet)
- Reprezentacja intensywności dźwięku (decybele)
- Pomiar trzęsień ziemi (skala Richtera)
- Analizy finansowe i demograficzne (np. przyrost populacji)
Praktyczne zastosowania logarytmów
Nauki ścisłe i inżynieria
- Chemia: obliczanie pH, kinetyka reakcji chemicznych
- Fizyka: wzrost wykładniczy, rozpad promieniotwórczy
- Akustyka: pomiar natężenia dźwięku (decybele)
- Elektronika: obliczanie wzmocnienia, spadku napięcia
Informatyka i matematyka
- Analiza algorytmów: złożoność obliczeniowa (np. O(log n))
- Kompresja danych: kodowanie obrazów, dźwięku
- Teoria informacji: entropia, ilość informacji
- Kryptografia: funkcje jednokierunkowe, bezpieczeństwo
Przykłady obliczania logarytmów
| Operacja | Wzór | Wartość | Wyjaśnienie |
|---|---|---|---|
| Logarytm dziesiętny z 1000 | log10 1000 | 3 | 103 = 1000 |
| Logarytm naturalny z e5 | ln(e5) | 5 | e5 ≈ 148.4 |
| Logarytm o podstawie 2 z 32 | log2 32 | 5 | 25 = 32 |
| Logarytm dziesiętny z 0.01 | log10 0.01 | -2 | 10-2 = 0.01 |
| Logarytm o podstawie 3 z 81 | log3 81 | 4 | 34 = 81 |
Podsumowanie
Kalkulator logarytmów to wszechstronne narzędzie dla uczniów, studentów, naukowców i profesjonalistów z różnych dziedzin. Dzięki niemu możesz:
- Błyskawicznie obliczać logarytmy o dowolnej podstawie
- Otrzymywać precyzyjne wyniki z kontrolowaną dokładnością
- Rozwiązywać zadania z matematyki na różnych poziomach edukacji
- Wspierać praktyczne obliczenia w naukach ścisłych i inżynierii
Logarytmy, choć początkowo mogą wydawać się skomplikowane, są fundamentalnym narzędziem w matematyce i naukach stosowanych. Nasz kalkulator sprawia, że praca z logarytmami staje się prosta i intuicyjna, pozwalając skupić się na zrozumieniu koncepcji, a nie na żmudnych obliczeniach.